This is an old post from August 9th, 2010

I recently had to build an optimized Sudoku puzzle solver for a homework which turned into a contest between students. I was part of a team of three and we competed again six similar teams… And we won! Here, I will discuss the algorithm we used.

The problem context

First, the Sudoku grid is provided as a simple text file like this example.

The position of each digits is just the same as on the Sudoku grid and a zero represents an unknown value (which the algorithm must figure out). The files always ends with an extra line break after the last line and contains no unnecessary white-space. This is important, otherwise the program return an error message. This example maps to the following Sudoku grid.

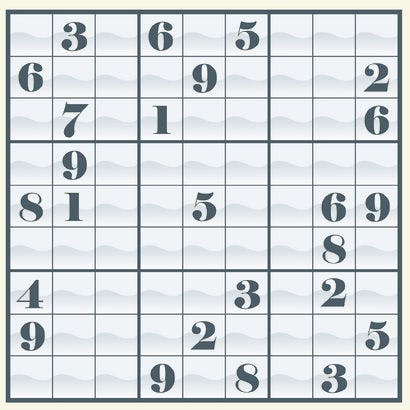
The time spent to read and parse the problem file is not counted towards the algorithm’s total resolution time.

The algorithm must be implemented in Java and was to be run on a Quad core 3.2 GHz with 4 GB RAM, but we did not take advantage of multithreading because of the thread creation overhead. For example, on my machine, resolving the example Sudoku takes anywhere between 1 and 3 milliseconds while creating a thread and switching to it takes at least 0.5 millisecond. Here is the code used to test the overhead.

final long time = System.nanoTime();

Thread thread = new Thread() {
    @Override
    public void run() {
        System.out.println("end: " + (System.nanoTime() - time));
    }
};

thread.run();

try {
    thread.join();
}
catch (InterruptedException ex) {}

Another aspect of the problem context is very important as it allowed us to forget about an edge case in which our algorithm does not perform well. The assumption is that the Sudoku grid is always set to have only one solution. This makes a common backtracking only algorithms take a lot more time than our solution. Such an algorithm would be better suited to calculate one possible solution for an empty or almost empty board. On the other hand, our algorithm which makes a lot of rules based decisions is unable to efficiently apply rules in such an open-ended scenario and thus spends considerably more time on an empty board than a naive backtracking algorithm does.

Explaining the basic rules of Sudoku is quite outside the scope of this post, but here I will define a few terms for the sake of clarity.

“Sections” are the 3×3 sub-grids (often separated by darker lines on Sudoku boards) “Numbers”, “digits” or “values” are the numerals from 1 through 9 that are placed on the board. On our board, zero means an unknown value. “Square” or “position” represents the location of a digit determined by its x and y coordinates.

Representing the board

We have chosen to represent the board as an 9×9 integer matrix. As we discovered later, this is not the most efficient solution. Java treats a two dimensional array as an array of arrays. This means accessing a cell in a matrix costs twice the time of accessing an element in an array, once for the column and once for the row. Unlike C++ and C#, Java does not support real multidimensional arrays. In light of this, we should have used a single dimension array.

In any case, we used a 9×9 integer matrix to represent the board as in the file, thus zero means the digits at this position is unknown. Accompanying the board is the “allowedValues” matrix. This matrix contains all the possible values for each position in a 9×9 matrix of integer bit fields. For each of these bit field, it is possible to determine if a certain “value” is legal using this calculation.

boolean isValueLegal = ((allowedValues[x][y] & (1 << (value - 1))) != 0);

In practice, we determined that it was more efficient to cache the possible masks into a static array called “allowedBitFields”. I would have thought accessing the value in the array would have taken longer than these mathematical operations, but profiling proved me wrong (likely due to the JIT compiler optimizing behind the scenes since the cache array is final).

Code structure

For the sake of efficiency, we created a single SudokuSolver class with only static private final methods and properties so there is no state for the program to manage (except for “main”, obviously). We also made heavy use of final method arguments and variables whenever possible.

Some loops even declare a final variable to hold the current iterated value if it was used enough for a performance gain to be measurable. Consider this method which applies the correct value for every square which have only one possible value left according to the “allowedValues” matrix.

private final static int moveNothingElseAllowed(final int[][] board,
        final int[][] allowedValues) {

    int moveCount = 0;

    for (int x = 0; x < 9; x++) {
        final int[] allowedValuesRow = allowedValues[x];

        for (int y = 0; y < 9; y++) {
            final int currentAllowedValues = allowedValuesRow[y];

            if (countSetBits(currentAllowedValues) == 1) {
                setValue(board, allowedValues, getLastSetBitIndex(
                        currentAllowedValues), x, y);

                moveCount++;
            }
        }
    }

    return moveCount;
}

The algorithm

The whole magic starts with the “solveBoard” method. It has two types of tools at its disposal to solve a Sudoku puzzle: rules and hypothesis (or brute force). An hypothesis is the equivalent of the common backtracking solution. We set a hypothesis such as the value of a square among the available values and then try to solve the modified board. If we cannot, then that was not a valid move, so we try another instead. If the program tries all the possible values for a square and none succeeds, then it declares the puzzle impossible to crack.

Using hypothesis only is very inefficient. We already know from the way people solve Sudoku puzzles that many moves can be logically deduced from the position. Thus, we implemented four rules that were shown to reduce the time taken to solve most puzzles. These are as follow:

No other value is allowed according to the allowed values matrix.
A certain value is allowed in no other square in the same section.
A certain value is allowed in no other square in the same row or column.
A certain value is allowed only on one column or row inside a section, thus we can eliminate this value from that row or column in the other sections.

Rules 2 and 3 are very similar and may benefit from being merged together as a single rule. However, they are not the same as rule 1 which only checks the “allowedValues” matrix to see if a position allows only one value and sets it. It is very fast. Rules 2 and 3 instead goes on all positions on the board, and for every legal value for these positions, checks if any other positions on the same row, column or section allow that value. If no other position the row (for example) allow a certain value, then we can be certain that the position we are testing has that value.

This diagram illustrates rule 2. The small numbers in each square represent the legal values for each position.

Example of rule #2

In the top left square, there were multiple possible values, but since “2” was allowed in no other square, then we can safely say that “2” belongs to the top left square. The same logic applies to rows and columns and is implemented as rule 3.

As for rule 4, it is the most complex of our rules and has the lowest benefits. Yet, in most Sudoku puzzles, it still improves performance, even if by a lower margin than the other rules. This diagram shows an application of this rule.

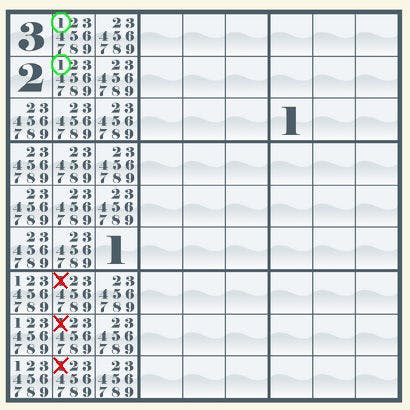
Example for rule #4

As we can see, in the top left section, the value “1” is allowed only in the second column. This means “1” is forced to be in that column, even if we do not know what row it is in. Using this property, we can remove “1” from the possible values in the same column in other sections. This rule does not let us set values directly. It simply supports the first three rules.

The program runs these four rules in a loop. We have witnessed that, whenever an iteration places less than four values, then it is more efficient to attempt a hypothesis than to continue using the rules. After doing a hypothesis, the program calls the “solveBoard” method recursively and runs the rules on the “test” board.

The legal stuff and acknowledgements

As everything provided on this site, you are free to do whatever you want with it. You don’t even have to mention me (although I’ll appreciate it). However, I’ll ask for one thing in return… If it doesn’t work, don’t sue me! Really, I provide no implied warranty, guarantee of fitness for any purpose or whatsoever. If you have any issue using it, post a comment and I’ll help you out because I’m a nice guy (!), but unless you’re willing to pay me for it, I won’t work for you… probably (I’m a really nice guy).

Also, thanks to my teammates on this project: Mathieu Lacasse-Potvin and Michael Badeau.

The program was part of an assignment for the class LOG320 at École de Technologie Supérieure in Montréal during summer 2010.

The code

The original version of the code is now available on Github : SudokuSolverV1

An updated version of this algorithm is upcoming...

Sudoku solver

Table of contents